Lesson Outline and Objective
Students will be able to deduce properties of shapes drawn on a coordinate grid.
The tangram is a traditional puzzle made up of seven polygons which can be put together to form a square, as well as being assembled into countless other shapes. There are lots of ways in which the tangram pieces can be explored mathematically. In this lesson, students explore the creative opportunities the tangrams provide while working within the coordinate grid system and reviewing names for different polygons. At mathigon.org/tangram, students can use tangrams to make a variety of shapes out of tangrams.
Warm Up
In this polypad canvas, students are invited to work out the coordinates of the seven tangram pieces arranged in a square. Students can move the pieces around as needed.
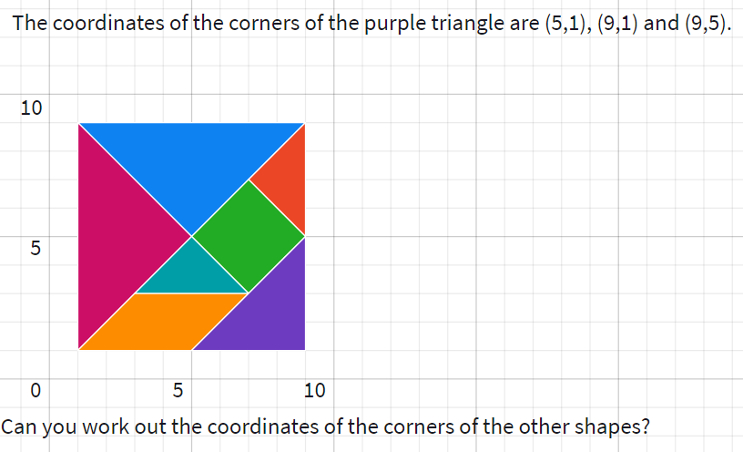
Solutions:
- Large Pink Triangle (1,1), (1.9), (5,5)
- Large Blue Triangle (1,9), (9,9), (5,5)
- Small Turquoise Triangle (3,3), (7,3), (5,5)
- Small Red Triangle (9,5), (9,9), (7,7)
- Green Square (5,5), (7,3), (9,5), (7,7)
- Orange Parallelogram (1,1), (5,1), (7,3), (3,3)
Main Activity
There are several different ways to approach this lesson with the tangram pieces. One possibility is to pose an open question for exploration:
- Which quadrilaterals can you make using two or more tangram pieces?
This might be suitable for students who are used to working independently or in small groups on an investigative task. You may need to have a discussion about whether pieces can be reused within a shape or not.
A more scaffolded approach could be to start by inviting students to list the quadrilaterals that they know and describe their properties. Then, challenge them to make a square (other than the original square which uses all seven pieces), a rectangle, a parallelogram and a trapezium (UK) / trapezoid (US). Once they have made their shapes on Polypad, invite them to work out the coordinates of each corner of their finished shapes, choosing an origin and drawing a separate axis for each shape they make. Care will need to be taken to make sure the shapes have their corners on grid points. For example, the image below shows a rectangle which needs to be at a 45° angle for all the vertices to be on the grid.

Once they have made a shape, they could challenge their classmates to plot the coordinates and draw an outline of the shape, and then work out which tangram pieces can fill in the outline.
Discussion throughout the lesson could focus on the following talking points:
- How do you know the shape is a square/rectangle/parallelogram/trapezium (trapezoid)?
- How do you know which lines are parallel/perpendicular/the same length?
- Are there any shapes that we can make in more than one way?
- Could we work out the area of any of the shapes we have made?
- Can we make a rhombus (other than the squares)?
Possible Solutions
This Polypad canvas shows some examples of quadrilaterals that students may discover. The tangram shapes have the following areas:
- Large triangles: 16 square units
- Medium triangle: 8 square units
- Small triangle: 4 square units
- Parallelogram: 8 square units
- Square: 8 square units
Students could calculate these areas using the area formulas for each shape, or by working out the areas relative to the small triangles by considering how many small triangles make up each of the other shapes. This could also lead into a discussion of fractions by considering the individual shapes that make up larger shapes.
Support and Extension
Lining up the corners on grid points may be challenging for some students. Consider creating some quadrilaterals, draw around them with the pen, and then erase the shapes that made them. See this Polypad for an example:
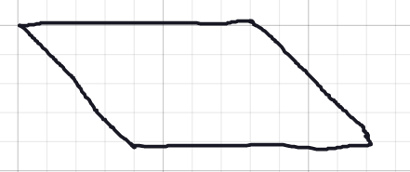
You could also give clues such as “This shape can be made with two tangram pieces”.
A suitable extension could be to explore the side lengths of the shapes they can make in order to get some insight into shapes that they cannot make. Students may initially believe that they can make a rhombus:
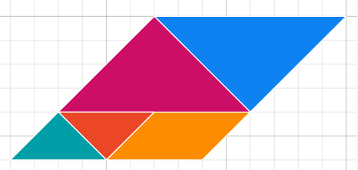
For students who have met Pythagoras’s Theorem, they could work out that in fact the sides are 8 units and units (8.5 units to 1 decimal place).