FractalesL'ensemble Mandelbrot

Toutes les fractales que nous avons vues dans les chapitres précédents ont été créées en utilisant un processus d'itération: vous commencez avec un motif spécifique, puis vous le répétez encore et encore.

Ceci est similaire à un autre concept en mathématiques que vous avez vu auparavant: avec séquences récursives, vous commencez avec un nombre spécifique, puis vous appliquez la même formule récursive, encore et encore, pour obtenir le nombre suivant dans le séquence.

Prenons l'exemple de la formule récursive xn=xn−12 et traçons ses termes sur une droite numérique. Vous pouvez modifier la valeur de x0:

Remarquez comment la séquence résultante peut se comporter très différemment, selon la valeur de départ x0:

Jusqu'à présent, nous n'avons rien appris de nouveau. Cependant, il y a environ un siècle, les mathématiciens ont commencé à explorer ce qui arrive à ces séquences si vous utilisez des nombres complexes, plutôt que simplement la vraie ligne numérique. Leurs découvertes ont été parmi les résultats les plus surprenants et les plus beaux de toutes les mathématiques.

Julia Sets

Utilisons la même séquence que précédemment, xn=xn−12, mais sur le plan complexe. Vous pouvez déplacer la position de x0, pour voir ce qu'il advient des termes suivants. Si la séquence semble converger, colorions le point correspondant sur le plan en bleu:

Comme vous pouvez le voir, la séquence converge tant que x0 se trouve à l'intérieur du cercle unitaire outside the unit squareabove the >>>>x<<<<-axis (le cercle de rayon 1, centré à l'origine).

Maintenant, rendons les choses un peu plus difficiles. Plutôt que de mettre au carré le nombre précédent, nous ajoutons également une constante c à chaque fois (qui peut être n'importe quel nombre complexe). En d'autres termes, xn=xn−12+c. Pensez-vous que nous aurons toujours un cercle de convergence? Quelles autres formes pensez-vous que nous pourrions voir? Continuer

Dans ce diagramme, vous pouvez déplacer la position de x0 ainsi que la valeur de c:

Les différentes formes formées par la coloration des nombres sont appelées Julia Sets. Ils ont été découverts indépendamment par deux mathématiciens français, Gaston Julia et Pierre Fatou, vers 1918.

À cette époque, aucun ordinateur ne permettait de visualiser à quoi ressemblaient les ensembles Julia. Des mathématiciens comme Julia et Fatou ont pu raisonner mathématiquement à leur sujet, mais ils n'ont vu que des croquis rugueux et dessinés à la main de ce à quoi ils pourraient ressembler.

Nous n'avons pas ce problème aujourd'hui - les images ci-dessous sont toutes des ensembles Julia différents. Les différentes couleurs indiquent la vitesse à laquelle la séquence à ce point diverge:

Continuer

L'ensemble Mandelbrot

Lors de la création des différents ensembles de Julia, vous avez peut-être remarqué qu'il y avait certaines valeurs de c pour lesquelles chaque séquence diverge et le plan complexe entier reste blanc. Quelques décennies après Julia et Fatou, une nouvelle génération de mathématiciens a tenté de cartographier à quoi ressemblaient ces domaines.

Dans l'exemple précédent, nous avons choisi une valeur fixe pour c, puis changé la position de x0 pour colorer le plan. Maintenant, fixons la valeur de x0=0 et modifions plutôt la valeur de c.

Encore une fois, peignez sur le plan complexe pour révéler la zone dans laquelle les séquences restent délimitées. Quelles formes attendez-vous à apparaître?

xn=xn−12+${complex(c)}

x0=${complex(x0)}

x1=${complex(x1)}

x2=${complex(x2)}

x3=${complex(x3)}

…Bounded!Diverges!

Cette fractale est appelée Mandelbrot Set, et lorsqu'elle est tournée de 90 °, elle ressemble presque à une personne, avec la tête, le corps et les deux bras. Il a été défini et dessiné pour la première fois en 1978, dans un document de recherche des mathématiciens Robert Brooks et Peter Matelski:

Quelques années plus tard, Benoit Mandelbrot a utilisé les puissants ordinateurs d'IBM pour créer une visualisation beaucoup plus détaillée de la fractale, qui portera plus tard son nom. Les premières impressions semblaient différentes de ce à quoi il s'attendait - jusqu'à ce qu'il se rende compte que les techniciens travaillant sur les imprimantes nettoyaient le «flou» autour de son bord, en supposant qu'il était causé par des particules de poussière ou des erreurs d'imprimante, et non une caractéristique déterminante des fractales ! Continuer

Comme toutes les fractales, nous pouvons «zoomer» sur l'ensemble de Mandelbrot pour toujours, trouver de nouveaux motifs à toutes les échelles. Ici, vous pouvez zoomer sur une partie de l'ensemble de Mandelbrot appelée Seahorse valley. Les points noirs sont à l'intérieur de l'ensemble de Mandelbrot, où la séquence est limitée. Les points colorés sont en dehors de l'ensemble de Mandelbrot, où la séquence diverge et les différentes couleurs indiquent la vitesse à laquelle elle se développe à l'infini:

Scale: ${pow(scale)}

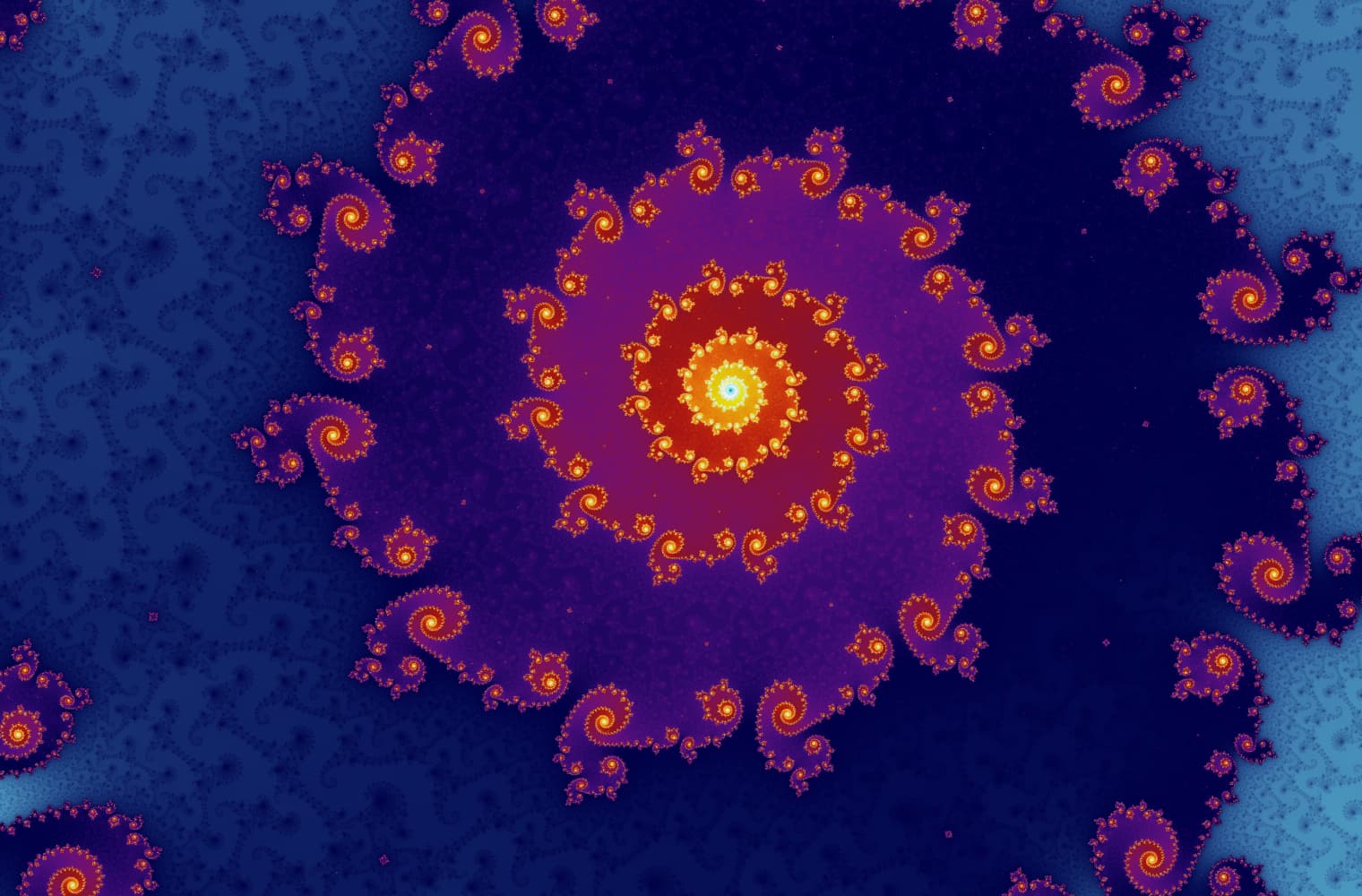
Ce curseur se compose de 27 images individuelles, jusqu'à un niveau de zoom supérieur à 14 quadrillions, ou 254. Au total, il a fallu près de 45 minutes pour effectuer le rendu sur un ordinateur portable moderne. L'ensemble de Mandelbrot peut être créé avec une seule équation simple, xn=xn−12+c, mais il est infiniment complexe et incroyablement beau.

Lorsque vous déplacez la valeur de c autour de l'ensemble Mandelbrot, vous remarquerez peut-être une propriété curieuse:

• Toutes les séquences du corps principal de l'ensemble de Mandelbrot convergentdivergereach an orbit en un seul point.
• Les séquences de la grosse ampoule en haut atteignent une orbiteconvergediverge composée de points.
• Les séquences de cette ampoule plus petite ont des orbites de longueur .

Chaque ampoule a une orbite de taille différente, les ampoules plus petites ayant de plus en plus de points sur leurs orbites. La taille de ces orbites est étroitement liée à la carte logistique, un concept important de la théorie du chaos.