Transformations et symétrieGroupes de symétrie et fonds d'écran
Certaines formes ont plus d'une symétrie - jetons un œil au








Vous avez déjà montré ci-dessus qu'un carré a
Il présente également une symétrie de rotation de
Et enfin, nous pouvons penser à «ne rien faire» comme un autre type particulier de symétrie - parce que le résultat est (évidemment) le même qu'avant. C'est ce qu'on appelle parfois l' identité .
Au total, nous avons trouvé
Maintenant, nous pouvons réellement commencer à faire de l'arithmétique avec ces symétries. Par exemple, nous pouvons ajouter deux symétries pour en obtenir de nouvelles:






Chaque fois que vous ajoutez deux symétries d'un carré, vous en obtenez une nouvelle. Voici un "calculateur de symétrie" où vous pouvez l'essayer vous-même:
Passez du temps à jouer avec la calculatrice de symétrie et essayez de trouver des motifs. Pouvez-vous compléter ces observations?
- Ajouter deux rotations donnera toujours
(ou l'identité). * L'ajout de deux réflexions donnera toujours (ou l'identité). * L'ajout des deux mêmes symétries dans l'ordre opposé résultat. * L'ajout de l'identité .
Vous vous êtes peut-être déjà rendu compte que l'ajout symétries est en fait très similaire à l'ajout entiers :
- Adding two symmetries/integers always gives another symmetry/integer:
+ = 12 + 7 = 19 - Adding symmetries/integers is
associative :+ + = + + 4 + 2 + 5 = 4 + 2 + 5 - Every symmetry/integer has an inverse, another symmetry/integer which, when added, gives the identity:
+ = 4 + –4 = 0
En mathématiques, toute collection possédant ces propriétés est appelée un
Dans cet exemple, nous avons commencé avec les huit symétries du carré. En fait, chaque forme géométrique possède son propre groupe de symétrie . Ils ont tous des éléments différents, mais ils satisfont toujours aux trois règles ci-dessus.
Les groupes apparaissent partout en mathématiques. Les éléments peuvent être des nombres ou des symétries, mais aussi des polynômes, permutations, matrices, fonctions… tout ce qui obéit aux trois règles. L'idée clé de la théorie des groupes est que nous ne nous intéressons pas aux éléments individuels, juste à la façon dont ils interagissent les uns avec les autres .
Par exemple, les groupes de symétrie de différentes molécules peuvent aider les scientifiques à prédire et expliquer les propriétés des matériaux correspondants.
Les groupes peuvent également être utilisés pour analyser la stratégie gagnante dans les jeux de société, le comportement des virus en médecine, les différentes harmonies musicales et bien d'autres concepts…
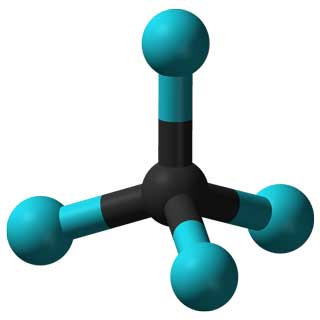
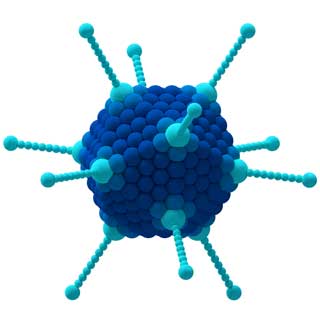
Les propriétés de la molécule CCl 4 (à gauche) et de l'adénovirus (à droite) sont déterminées par leurs symétries.
Groupes de papiers peints
Dans les sections précédentes, nous avons vu deux types de symétrie différents correspondant à deux transformations différentes: les rotations et les réflexions. Mais il y a aussi une symétrie pour le troisième type de transformation rigide: les


Honyecomb hexagonal


Carrelage mural en céramique
En plus de la symétrie réflexionnelle, rotationnelle et translationnelle, il existe même un quatrième type: les


Un motif peut avoir plusieurs types de symétrie. Et tout comme pour les carrés, nous pouvons trouver le
Ces groupes ne vous disent pas grand-chose à quoi ressemble le motif (par exemple ses couleurs et ses formes), juste comment il est répété . Plusieurs motifs différents peuvent avoir le même groupe de symétrie - tant qu'ils sont organisés et répétés de la même manière.


Ces deux motifs ont les mêmes symétries, même s'ils sont très différents. Mais les symétries ne concernent pas les couleurs ou les formes superficielles.


Ces deux motifs ont également les mêmes symétries - même s'ils se ressemblent plus aux motifs correspondants à gauche qu'entre eux.
Il s'avère que, bien qu'il existe une infinité de modèles possibles, ils ont tous l'un des 17 groupes de symétrie différents. Ceux-ci sont appelés les groupes de papier peint . Chaque groupe de papier peint est défini par une combinaison de translations, rotations, réflexions et réflexions de glissement. Pouvez-vous voir les

Group 1 – P1
Only translations div img(src="/content/transformations/images/wallpapers/p2.svg" width=360, height=240) p.caption Group 2 – P2 Rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p3.svg" width=360, height=240) p.caption Group 3 – P3 Rotations of order 3 (120°), translations div img(src="/content/transformations/images/wallpapers/p4.svg" width=360, height=240) p.caption Group 4 – P4 Four rotations of order 2 (180°), translations div img(src="/content/transformations/images/wallpapers/p6.svg" width=360, height=240) p.caption Group 5 – P6 Rotations of order 2, 3 and 6 (60°), translations div img(src="/content/transformations/images/wallpapers/pm.svg" width=360, height=240) p.caption Group 6 – PM Parallel axes of reflection, translations div img(src="/content/transformations/images/wallpapers/pmm.svg" width=360, height=240) p.caption Group 7 – PMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/p4m.svg" width=360, height=240) p.caption Group 8 – P4M Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p6m.svg" width=360, height=240) p.caption Group 9 – P6M Rotations (ord 2 + 6), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p3m1.svg" width=360, height=240) p.caption Group 10 – P3M1 Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p31m.svg" width=360, height=240) p.caption Group 11 – P31M Rotations of order 3, reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/p4g.svg" width=360, height=240) p.caption Group 12 – P4G Rotations (ord 2 + 4), reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/cmm.svg" width=360, height=240) p.caption Group 13 – CMM Perpendicular reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pmg.svg" width=360, height=240) p.caption Group 14 – PMG Reflections, glide reflections, rotations of order 2, translations div img(src="/content/transformations/images/wallpapers/pg.svg" width=360, height=240) p.caption Group 15 – PG Parallel glide reflections, translations div img(src="/content/transformations/images/wallpapers/cm.svg" width=360, height=240) p.caption Group 16 – CM Reflections, glide reflections, translations div img(src="/content/transformations/images/wallpapers/pgg.svg" width=360, height=240) p.caption Group 17 – PGG Perpendicular glide reflections, rotations of order 2, translations
Malheureusement, il n'y a pas de raison simple pour laquelle il y a 17 de ces groupes, et prouver qu'il nécessite des mathématiques plus avancées. Au lieu de cela, vous pouvez essayer de dessiner vos propres motifs répétés pour chacun des 17 groupes de fonds d'écran:
Examples of other students’ drawings



Les groupes de papier peint étaient tous sur des motifs plats et bidimensionnels. Nous pouvons faire quelque chose de similaire pour les modèles tridimensionnels: ceux-ci sont appelés groupes cristallographiques, et il y en a 219!
En plus des translations, des réflexions, des rotations et des réflexions de glissement, ces groupes incluent des symétries comme des plans de glissement et des axes de vis (pensez au mouvement lorsque vous dévissez une bouteille).
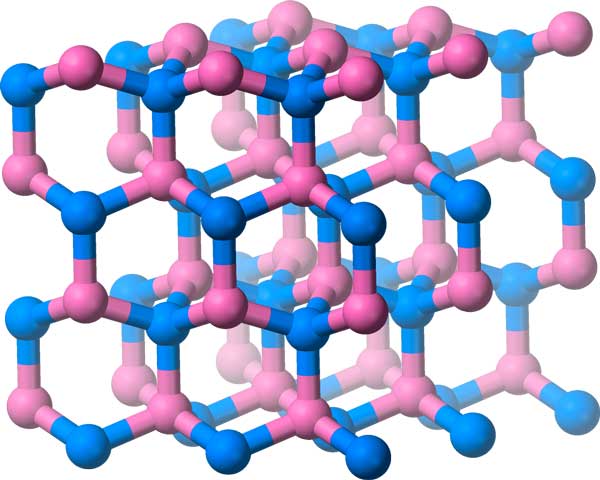
Le nitrure de bore a ses molécules disposées dans ce réseau cristallin, qui a un groupe de symétrie en trois dimensions.